数学分析-实数集与函数
 拉大锯
发表于
2020-01-06 09:10
4628
拉大锯
发表于
2020-01-06 09:10
4628实数集与函数
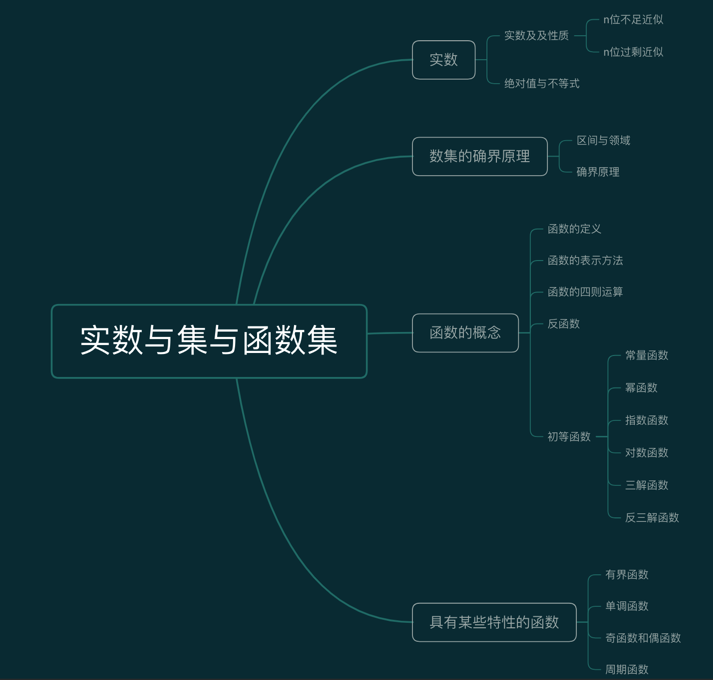
实数
实数由有理数和无理数两部分组成
-
有理数:可以用分数形式p/q(p,q为整数,q!=0)来表示。也可以用有限十进制小数或者无限十进制循环小数来表示。
-
无理数:无限十进不循环小数为无理数。
有有限小数也可以表示成无限小数。
比如说:2.001记为2.0009999999.....
比如说:-8记为-7.9999999999.....
比如说:0记为0.0000.....
也就是说,任何一个实数,都可以用一个确定的无限小数来表示。
- n位不足近似与n位过剩近似
假设X=a0·a1·a2...an为非负实数,那么我们称有理数Xn=a0·a1·a2...an为实数X的n位不足近似,而有理数Xn拔=Xn+1/10的n次方为X的n位过剩近似。
什么意思呢?
比如说,实数X = 10.01,那么10.009999为10.01的6位不足近似。而10.01+0.02=10.02为10.01的2位过剩近似。
而负实数则相反。
命题:x = a0a1a2a3....an与y=a0a1a2...an为两个实数,则x>y的等价条件存在非负整数n使得xn>yn拔
也就是x的n位不足近似>y的n位过剩近似。
eg: 设x,y为实属,x<y,证明:存在有理数r满足:
x<r<y
证明:
由于x<y,故存在xn拔<yn,n为非负整数。
令r=1/2(xn拔<+yn),由定义有理数可以表示为p/q,q不为0,q,p为整数,那么r为有理数。
实数的性质
- 实数的四则运算,加减乘除(除数不为0)是封闭的,也就是运算结果仍然是实数;
- 实数集是有序的,也就是ab两个实九必须满足a=b,或者a>b,或者a<b;
- 实数的大小具有传递性,也就是a>b,b>c那么a>c
- 实数具有阿基米德性,也就是任意的实数a,b,如果b>a>0,那么存在整数n使得na>b;
- 实数集具有稠密性,也就是说任意的两个实数间,一定存在另外一个实数,这个实数可以是有理数,也可以是无理数;
- 实数集与数轴成映射关系,也就是所有的实数都在在数轴上找到对应的位置。
阿基米德性
什么是阿基米德性呢?
对于任何a,b$\in$R,若b>a>0,则存在正整数n使得na>b>=(n-1)a
eg:设a,b属于实数集,证明:若对任何正数ε,有a<b+ε,则a<=b
这里要理解的是ε这个玩意儿,是可大可小的,所以证明时是一个好用的东西
可以使用反证法来证明。
若结论不成立,那么根据实数集的性质,有序性,则有a>b,令ε=a-b,则ε为正数且a=b+ε,但这与假设的a<b+ε相矛盾,所以a<=b成立。
绝对值与不等式
$|a| =\begin{cases} a,a>=0\ -a,a<0 \end{cases}$
数轴上绝对值的含义
数轴上绝对值的含义就是点a到原点的距离为$|a|$
- 实数的绝对值性质
- $|a|$=$|-a|$>=0;当且仅当a=0时有$|a|$ = 0
- -$|a|$<=a<=$|a|$
- $|a|$<h $\iff$
